Para firmar os princípios de projeto de treliças espaciais é útil o desenvolvimento de alguns conceitos ligados à geometria.
A formação das malhas é desenhada a partir de polígonos regulares, principalmente triângulos, quadrados, retângulos e hexágonos e octógonos. É importante observar que as malhas internas e externas não devem ser, obrigatoriamente, iguais ou unidirecionais, assunto que será amplamente desenvolvido no capítulo a seguir.
A formação de diagonais conduz a um conjunto de triângulos - equiláteros, isósceles e, excepcionalmente, retos ou escalenos.
O conjunto de diagonais conectadas com os polígonos das malhas, formam poliedros ou partes de poliedros. São importantes para o desenvolvimento de projetos de treliças espaciais os denominados sólidos platônicos ou poliedros regulares, pois possuem todas as faces, ângulos e ângulos entre faces iguais. Os poliedros regulares são formados a partir de triângulos, quadrados e pentágonos. Abaixo mostra-se, cada poliedro, as suas constantes geométricas, valores auxiliares para o desenho e cálculo das dimensões e ângulos da treliças espaciais, conforme apresentação do desenho 6:
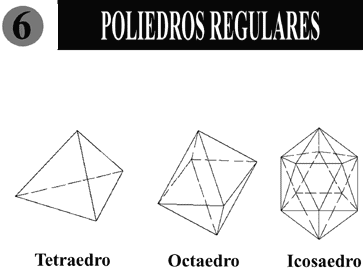
Desenho 6
Tetraedros - resultado de malhas formadas por triângulos, mais usados em estruturas planas;
4 nós
6 barras
4 faces
ângulo do diedro = 70o 32'
ângulo da face = 60 o
lado = 1
altura = 0,81650 (vértice ao centro da face oposta)
altura da fase = 0,8660
Octaedros - resultado de malhas formadas por quadrados, mais usados em estruturas planas.
6 nós
12 barras
8 faces
ângulo = 109 o 28'
ângulo da face = 60 o
lado = 1
altura = 0,7071 (vértice ao centro)
altura da face = 0,8660
Icosaedros - resultado de malhas formadas por pentágonos , mais usados em domos.
12 nós
30 barras
20 faces
ângulo do diedro = 138 o 11'
ângulo da face = 60 o
lado = 1
altura = 0,951069 (vértice ao centro)
altura da face = 0,8660
Outros poliedros regulares são o cubo e o dodecaedro, não utilizados em treliças espaciais devido a ausência de triângulação natural.

